一、实验目的
(1)了解变换域信息隐藏技术的基本原理
(2)掌握DCT信息隐藏的算法的实现和操作
参照上述程序编写的方法,参考课堂讲述以下数字水印嵌入方法,实现在lenna.bmp嵌入“复旦大学”。实现你的嵌入程序和提取程序。
二、实验过程
1、嵌入Hidefile.txt
(一种DCT变换数字水印方法.ppt上方法)
算法思路:
- 读入载体图像数据
- 将载体图像由真彩图像转换为灰度图像
- 将载体图像矩阵DCT变换
- 将秘密信息嵌入到到变换后的矩阵中
- 将矩阵反DCT变换,输出图片
- 作为检验,将嵌入结果输出
源代码:
% DCT信息隐藏
% 从文件中读取任意字符并将其隐藏在图像中
clc
clear
RGB=imread('Lenna.bmp'); % 装入图像
gray=rgb2gray(RGB); % 将真彩图像转换为灰度图像
J=dct2(gray); % 进行余弦变换
% 以下部分读入文本文件并保存在矩阵A中
fid=fopen('hidefile.txt','rt'); % 以文本方式只读
[A,count]=fread(fid);
fclose(fid);
[sizexA,sizeyA] = size(A);
sizeA = sizexA *sizeyA;
[m,n]=size(J); % 计算矩阵J的大小
gate=0.001; % 根据读入文件的大小决定gate的大小
while j < sizeA
j=0;
gate = gate + 0.001;
for i=1:m*n
if abs(J(i))<gate
j=j+1;
end
end
end
% 进行嵌入:
j=0;
for i=1:m*n
if abs(J(i)) < gate && j < sizeA
j=j+1;
s(j) = i;
J(i)=A(j); %将数组A的每一个字节嵌入到图片中
end
end
K=idct2(J)/255; % 进行余弦反变换
[sizexS,sizeyS] = size(s);
sizeS = sizexS *sizeyS;
for j=1:sizeA % 提取嵌入的sizeA个字节放到result数组中
result(j)=J(s(j));
end
% 将提取出来的结果输出到文件result.txt
fw=fopen('result.txt','w+');
fwrite(fw,result,'uint8');
fclose(fw);
% 显示图像
subplot(1,2,1),imshow(gray),title('原始图像');
subplot(1,2,2),imshow(K),title('嵌入水印后的图像');
其中,dct2是针对二维矩阵的处理函数,所以要先将原始的RGB图像转换为二维图像(这里先转换成灰度图像)。返回值dct中是灰度图gray的二维离散余弦变换。
结果如图所示:

第三张图片是使用对数刻度显示DCT变换后的图像,下图进行了着色,可以看到左上角能量最高,能量从左上角到右下角逐渐降低:
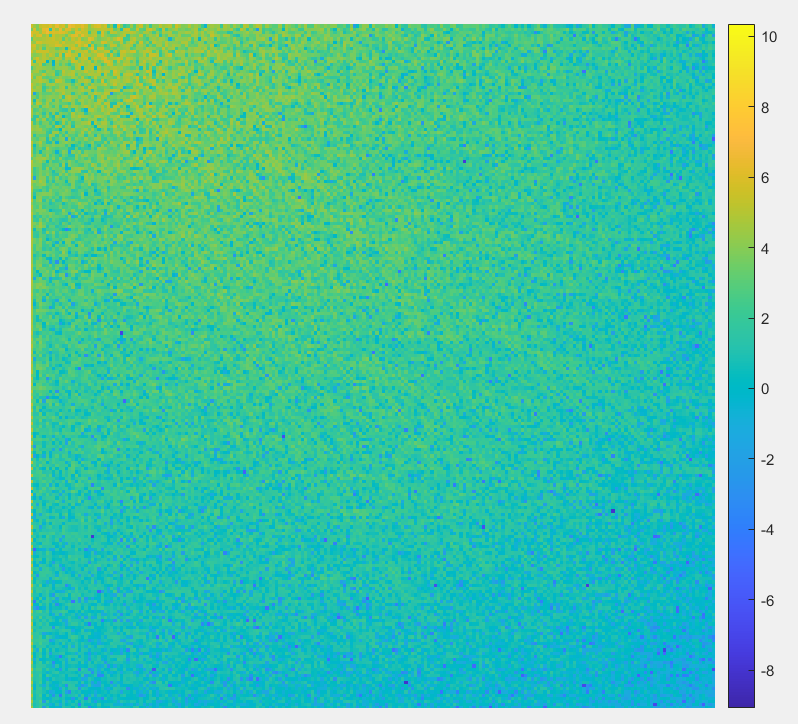
clc
clear
RGB=imread('Lenna.bmp'); % 装入图像
gray=rgb2gray(RGB); % 将真彩图像转换为灰度图像
J=dct2(gray); % 进行余弦变换
% subplot(1,3,1),imshow(RGB),title('原始图像');
% subplot(1,3,2),imshow(gray),title('灰度图');
% subplot(1,3,3),imshow(log(abs(J)),[]),title('DCT');
imshow(log(abs(J)),[])
colormap parula
colorbar
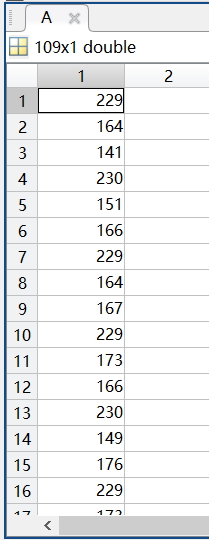
然后fread函数从fid中读取二进制数据并按列写入矩阵A,count参数返回成功读入的元素数量。
这里A是109*1的矩阵,count=109:
嵌入结果:

提取结果:

2、嵌入“复旦大学”
①处理载体图像
首先读入载体图像数据,将图像矩阵转为double型。因为做二维DCT变换,只需提取一层做隐藏,这里提取的是R层。
RGB=imread('Lenna.bmp'); % 装入图像
data0=double(RGB)/255; % 将图像矩阵转为double型,因为blkproc的参数要求是double型
data=data0(:,:,1); % 提取r通道做隐藏
T=dctmtx(8); % 产生8×8 DCT变换矩阵
DCTrgb=blkproc(data,[8 8],'P1*x*P2',T,T'); % 对分块图像做DCT变换
然后将256×256的载体图像分为8×8的块,做二维DCT变换。
分成8×8的小块有很多原因:
- 降低算法的复杂度
- 图像分块后,可以在每一块中编码一个秘密信息,增加隐藏信息的容量
- 为了与JPEG压缩方案相一致
- 避免全局变换有些情况下,会把前景物体当成高频去除(比如一个图像的前景物体是细微的波纹而背景是单一颜色的时候,前景就变成了高频分量很容易去掉)
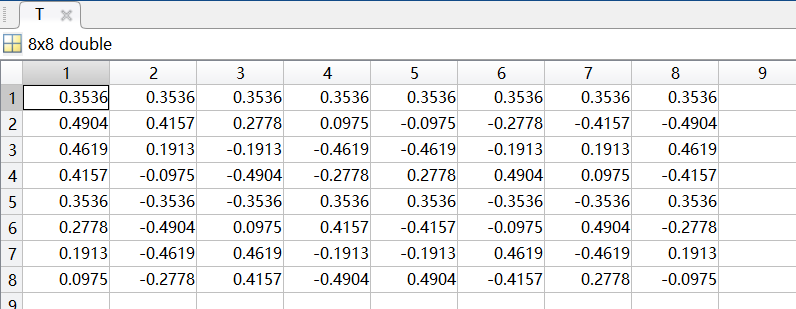
先用dctmtx(8),生成一个8×8 DCT变换矩阵T:
再通过blkproc(data,[8 8],'P1*x*P2',T,T')函数对分块图像做DCT变换。
调用形式为:
blkproc(A,[m n],fun, parameter1, parameter2, ...)
[m n]:图像以m*n为分块单位,对图像进行处理,这里是以8×8为分块单位fun:应用此函数对分别对每个m\*n分块的像素进行处理,即P1*x*P2是像素块的处理函数,其中x是每一个分成的8×8大小的块parameter1,parameter2:要传给fun函数的参数,即$p1=T$,$ p2=T’$,也就是$fun=p1xp2’=TxT’$的功能是进行离散余弦变换
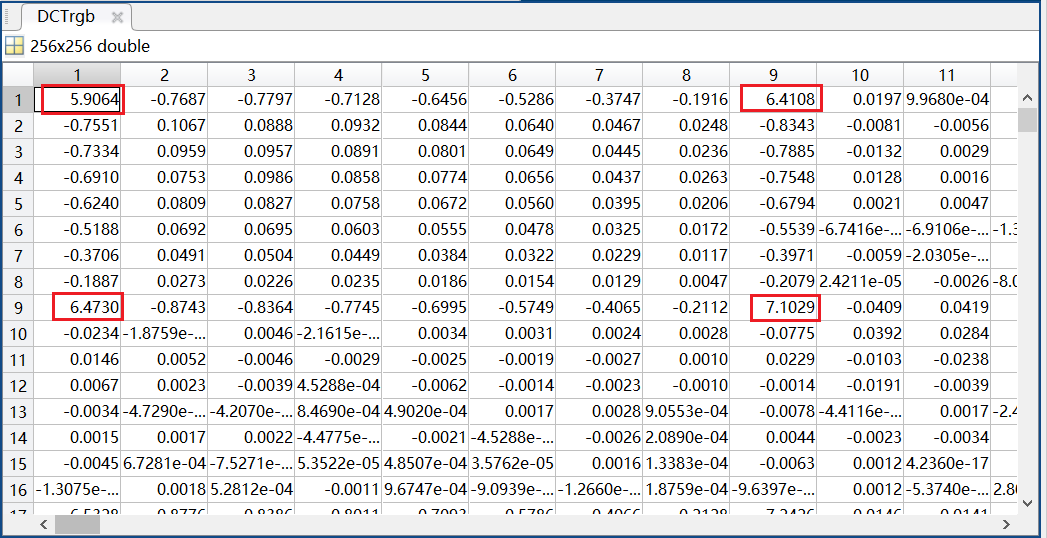
结果如图:

可以看到原本256×256的图像被分成了若干个8×8的块,每一块的左上角最亮,说明能量最高。
下表是DCTrgb矩阵的具体数据,可以看到每个8×8的小块中左上角的数字最大,同样说明该点(直流系数)能量最高。
②读取秘密信息

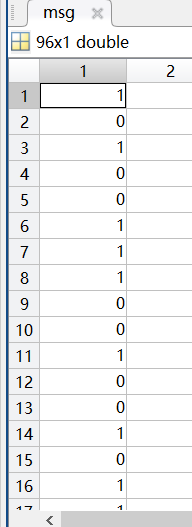
把“复旦大学”保存在secret.txt中,按位读取秘密信息:
fid=fopen('secret.txt','rt'); % 以文本方式只读
[msg,count]=fread(fid,'ubit1'); % 按位读取
fclose(fid);
可以看到读取的数据保存在96*1的矩阵中,总共读取了96位:
③随机选择块
水印算法为了平衡不可见性和鲁棒性,采取在中频部分嵌入水印,以一定的方式挑选一些中频系数,在这些中频系数中叠加秘密信息。挑选的方式可以是固定位置的中频系数,也可以是随机挑选。接下来的算法参考书上的,采用随机挑选的方法。
可以通过随机间隔法产生随机序列控制信息嵌入位,这样可以把秘密信息打散嵌入到图像中,使其不至于在一个局部形成明显的分界线;并且随机序列的种子可以作为密钥(因为对于相同的key,第一次调用rand产生的结果是相同的),保证了隐藏信息的安全性。
随机间隔法的思路是:利用随机数的大小控制前后2个嵌入位的距离。如一个长为$N$的服从$U(0,1)$的随机序列$R={r_1,r_2,…,r_N}$,$N$大于秘密信息长度,取第一个嵌入位为$i$,伪代码如下:
imbeding address = i
for (j = 1; j <= length(message); j++){
if (rj > 0.5)
imbeding address += k
else
imbeding address += p
}
定义: \(total=图像载体总像素点\\ quantity=为要选择的像素点\\ k=\lfloor \frac {total}{quantity} \rfloor+1\\ p=k-2\) 该算法通过判断相应的随机数与0.5的大小,
- 若$r_j>0.5$,则选择的嵌入位与前一个嵌入位间隔$k-1$位
- 若$r_j<0.5$,则选择的嵌入位与前一个嵌入位间隔$p-1$位
randinterval.m详细代码如下,细节实现见注释,其中用学号作为共享密钥:
%函数功能:本函数将利用随机序列进行间隔控制,选择消息隐藏位置
%输入格式举例:[row,col]=randinterval(test,60,1983)
%算法描述:
%输入:载体矩阵matrix、嵌入信息长度count(要选择的像素数量)、密钥key
%输出:嵌入位置的行向量row、列向量col
%步骤:
%1、根据载体矩阵获得矩阵大小,计算随机间隔k和p
%2、用密钥key产生一个长度为count的随机序列a
%3、设置长度均为count的行向量row和列向量col,用来保存嵌入位置,第一个位置都为1
%4、设置两个变量r、c存放当前嵌入位置,并初始化值都为1
%5、循环从2到L:
% 若随机数a(i)>0.5,则c=c+k;否则c=c+p
% 判断c?>n,若大于,则r=r+1(换行),若r>m,则嵌入信息超过了载体能嵌入的大小,报错
% c=mod(c,n);若c==0,则c=n(最后一个位置),进入下一行的第一列
% 将r,c赋给向量row和col中保存
function [row,col]=randinterval(matrix,count,key)
% 根据载体矩阵获得矩阵大小,计算随机间隔k和p
% 传入matrix是32*32,所以计算出k=11,p=9
[m,n]=size(matrix);
k=floor(m*n/count)+1;
p=k-2;
if p==0
error('载体大小不能将秘密信息隐藏进去!');
end
% 产生一个长度为count的随机序列
rand('seed',key);
a=rand(1,count);
% 初始化长度均为count的行向量row和列向量col
row=zeros([1,count]);
col=zeros([1,count]);
% 设置两个变量r、c存放当前嵌入位置
r=1;
c=1;
row(1,1)=r;
col(1,1)=c;
% 设置嵌入位置
for i=2:count
if a(i)>=0.5
c=c+k;
else
c=c+p;
end
if c>n
r=r+1; % 行数+1,换行
if r>m
error('载体大小不能将秘密信息隐藏进去!');
end
c=mod(c,n);
if c==0
c=1; % 进入下一行的第一列
end
end
row(1,i)=r;
col(1,i)=c;
end
根据学号生成的随机序列:
| 0.999992 | 0.868462 | 0.244395 | 0.54135 | 0.467233 | 0.781041 | 0.952955 | 0.321135 | 0.320704 | 0.065307 | 0.616498 | 0.480584 | 0.169035 | 0.965428 | 0.946538 | 0.4703 | 0.328851 | 0.992302 | 0.616584 | 0.933158 | 0.582514 | 0.313227 | 0.411023 | 0.069564 | 0.153833 | 0.473071 | 0.908035 | 0.346081 | 0.584001 | 0.298809 | 0.089679 | 0.237802 | 0.737547 | 0.952535 | 0.263918 | 0.671766 | 0.367361 | 0.24359 | 0.008963 | 0.634661 | 0.752961 | 0.01745 | 0.27734 | 0.246644 | 0.348481 | 0.927314 | 0.368365 | 0.115293 | 0.72729 | 0.563589 | 0.233505 | 0.522268 | 0.762226 | 0.725093 | 0.640735 | 0.833493 | 0.513483 | 0.102344 | 0.090792 | 0.939436 | 0.095347 | 0.495477 | 0.483708 | 0.680967 | 0.013358 | 0.506023 | 0.733855 | 0.909267 | 0.052236 | 0.926251 | 0.499293 | 0.615858 | 0.722918 | 0.086183 | 0.470253 | 0.535554 | 0.05902 | 0.949916 | 0.238486 | 0.229795 | 0.172183 | 0.874635 | 0.984132 | 0.311545 | 0.131753 | 0.370457 | 0.263775 | 0.274588 | 0.000542 | 0.111428 | 0.766805 | 0.693678 | 0.648985 | 0.486726 | 0.408886 | 0.154018 | | ——– | ——– | ——– | ——- | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | —— | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——- | ——– | ——– | ——– | ——- | ——- | ——– | ——– | ——– | ——– | ——– | ——- | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——- | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– | ——– |
通过调用randinterval,传入32*32的矩阵,返回随机选择嵌入的是哪几个8×8的块,并确定图像块的首地址。
% 产生随机的块选择,确定图像块的首地址
[row,col]=size(DCTrgb);
row=floor(row/8); % 分成了8×8的块,共32*32个8×8的块
col=floor(col/8);
a=zeros([row col]); % 32*32的矩阵
key=学号;
[k1,k2]=randinterval(a,count,key); % 返回随机选择嵌入的行标和列标(对应块)
for i=1:count % 确定图像块的首地址
k1(1,i)=(k1(1,i)-1)*8+1;
k2(1,i)=(k2(1,i)-1)*8+1;
end
randinterval函数返回的k1,k2,表示的是嵌入的哪几个32*32个8×8的块。
| k1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 10 | 10 | 11 | 11 | 11 | 12 | 12 | 12 | 13 | 13 | 13 | 13 | 14 | 14 | 14 | 15 | 15 | 15 | 16 | 16 | 16 | 17 | 17 | 17 | 18 | 18 | 18 | 19 | 19 | 19 | 19 | 20 | 20 | 20 | 21 | 21 | 21 | 22 | 22 | 22 | 23 | 23 | 23 | 24 | 24 | 24 | 24 | 25 | 25 | 25 | 26 | 26 | 26 | 27 | 27 | 27 | 27 | 28 | 28 | 28 | 29 | 29 | 29 | 30 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k2 | 1 | 12 | 21 | 32 | 9 | 20 | 31 | 8 | 17 | 26 | 5 | 14 | 23 | 2 | 13 | 22 | 31 | 10 | 21 | 32 | 11 | 20 | 29 | 6 | 15 | 24 | 3 | 12 | 23 | 32 | 9 | 18 | 29 | 8 | 17 | 28 | 5 | 14 | 23 | 2 | 13 | 22 | 31 | 8 | 17 | 28 | 5 | 14 | 25 | 4 | 13 | 24 | 3 | 14 | 25 | 4 | 15 | 24 | 1 | 12 | 21 | 30 | 7 | 18 | 27 | 6 | 17 | 28 | 5 | 16 | 25 | 4 | 15 | 24 | 1 | 12 | 21 | 32 | 9 | 18 | 27 | 6 | 17 | 26 | 3 | 12 | 21 | 30 | 7 | 16 | 27 | 6 | 17 | 26 | 3 | 12 |
之后计算图像块在总体256×256的载体图像上的首地址:
| k1 | 1 | 1 | 1 | 1 | 9 | 9 | 9 | 17 | 17 | 17 | 25 | 25 | 25 | 33 | 33 | 33 | 33 | 41 | 41 | 41 | 49 | 49 | 49 | 57 | 57 | 57 | 65 | 65 | 65 | 65 | 73 | 73 | 73 | 81 | 81 | 81 | 89 | 89 | 89 | 97 | 97 | 97 | 97 | 105 | 105 | 105 | 113 | 113 | 113 | 121 | 121 | 121 | 129 | 129 | 129 | 137 | 137 | 137 | 145 | 145 | 145 | 145 | 153 | 153 | 153 | 161 | 161 | 161 | 169 | 169 | 169 | 177 | 177 | 177 | 185 | 185 | 185 | 185 | 193 | 193 | 193 | 201 | 201 | 201 | 209 | 209 | 209 | 209 | 217 | 217 | 217 | 225 | 225 | 225 | 233 | 233 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k2 | 1 | 89 | 161 | 249 | 65 | 153 | 241 | 57 | 129 | 201 | 33 | 105 | 177 | 9 | 97 | 169 | 241 | 73 | 161 | 249 | 81 | 153 | 225 | 41 | 113 | 185 | 17 | 89 | 177 | 249 | 65 | 137 | 225 | 57 | 129 | 217 | 33 | 105 | 177 | 9 | 97 | 169 | 241 | 57 | 129 | 217 | 33 | 105 | 193 | 25 | 97 | 185 | 17 | 105 | 193 | 25 | 113 | 185 | 1 | 89 | 161 | 233 | 49 | 137 | 209 | 41 | 129 | 217 | 33 | 121 | 193 | 25 | 113 | 185 | 1 | 89 | 161 | 249 | 65 | 137 | 209 | 41 | 129 | 201 | 17 | 89 | 161 | 233 | 49 | 121 | 209 | 41 | 129 | 201 | 17 | 89 |
④信息嵌入
为了实现水印盲提取,利用DCT变换后系数间的大小关系添加水印信息,即可以通过调整图像块中两个DCT系数的相对大小来对秘密信息进行编码。
在信息嵌入的时候,采用随机控制的办法选取图像块$b_i$以表示第$i$个消息比特的编码空间。$B_i=DCT{b_i}$为图像块$b_i$经过DCT变换后的结果。嵌入时可以分别选择其中的两个位置,用$(u_1,v_1)$和$(u_2,v_2)$代表所选定的两个系数的坐标。
- 如果$B_i(u_1,v_1)>B_i(u_2,v_2)$,代表隐藏1,如果相反,则交换两系数
- 如果$B_i(u_1,v_1)<B_i(u_2,v_2)$,代表隐藏0,如果相反,则交换两系数
因为需要通过比较变换后的两个DCT系数来完成信息的隐藏,所以在传递秘密信息前,通信的双方就必须对要比较的两个位置达成一致。对于每一个8×8图像块,共有64个系数,为了隐藏信息的不可见性,要求在其中选择两个恰当的系数$a$,$b$,使得这两个位置上的数据在图像经过处理后差别不大。
在假定嵌入过程不会导致载体严重降质的情况下,选择系数基于以下两点准则:
-
选择在JPEG压缩算法中预定义的亮度量化值一样的那些系数。因为量化系数一致,充分表明了位于这两个位置的DCT系数在数量级上是一致的,若产生交换,对图像的破坏较小,保证了不可见性。

-
选择DCT系数中的中频系数,兼顾了机密信息隐藏的不可见性与鲁棒性。如果选择低频系数,由于其所相应的能量过大,秘密消息的不可见性差,如果选择高频系数,则能量最低,很容易被篡改,鲁棒性差(比如Jepg有损压缩等操作一般都是针对能量低的高频部分展开的)。中频系数的频率适中,既不会太容易被篡改,保证了鲁棒性,也不会能量太高,破坏不可见性。
综上,通常选择$(5,2)\&(4,3)$或者$(2,3)\&(4,1)$这一对系数。
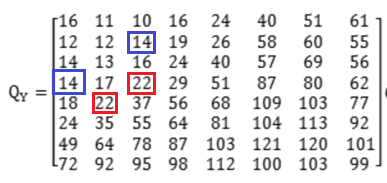
但由于这样的一对系数大小相差很少,往往难以保证隐秘图像在保存、信道上传输以及提取信息时再次被读取等过程中不发生变化。
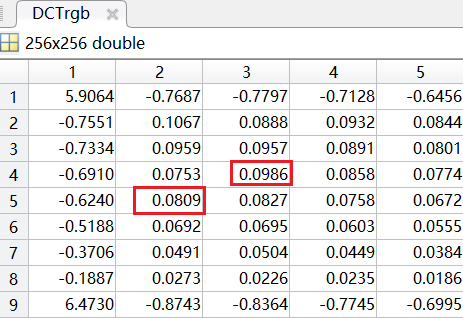
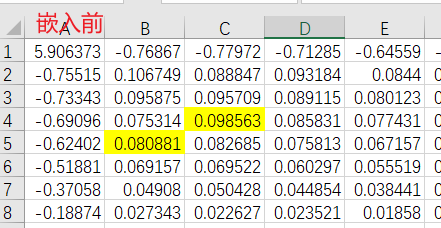
比如上图中,$B(5,2)=0.0809$,$B(4,3)=0.0986$。如果中间哪一个步骤引起了$10^-2$的小变化就会导致隐秘信息的丢失,因为会使得这两个系数的相对大小发生改变,就会直接影响编码的正确性。
| 所以,再引入一个控制量$α$对系数差值进行放大。在编码的过程中,无论是$B_i(u_1,v_1)>B_i(u_2,v_2)$,还是$B_i(u_1,v_1)<B_i(u_2,v_2)$,都要使得$ | B_i(u_1,v_1)-B_i(u_2,v_2) | >\alpha$,这样即使在变换过程中系数的值有轻微的改变,也不会影响编码的正确性。 |
算法中选择$(5,2)\&(4,3)$这一对系数,取$α=0.5$。
具体代码:
% 信息嵌入
temp=0;
alpha=0.5;
for i=1:count
if msg(i,1)==0 % 嵌入0,要求B(5,2)<B(4,3),若不满足则交换位置,因为k1(i)从1开始,所以是+4
if DCTrgb(k1(i)+4,k2(i)+1) > DCTrgb(k1(i)+3,k2(i)+2)
temp=DCTrgb(k1(i)+4,k2(i)+1);
DCTrgb(k1(i)+4,k2(i)+1)=DCTrgb(k1(i)+3,k2(i)+2);
DCTrgb(k1(i)+3,k2(i)+2)=temp;
end
else % 嵌入1,要求B(5,2)>B(4,3),若不满足则交换位置
if DCTrgb(k1(i)+4,k2(i)+1) < DCTrgb(k1(i)+3,k2(i)+2)
temp=DCTrgb(k1(i)+4,k2(i)+1);
DCTrgb(k1(i)+4,k2(i)+1)=DCTrgb(k1(i)+3,k2(i)+2);
DCTrgb(k1(i)+3,k2(i)+2)=temp;
end
end
% 要满足|B(5,2)-B(4,3)|>alpha,如果不满足,把小的系数调整的更小
diff=DCTrgb(k1(i)+4,k2(i)+1)-DCTrgb(k1(i)+3,k2(i)+2);
if diff>=-alpha && diff<=alpha
if diff<0 % B(5,2)小
DCTrgb(k1(i)+4,k2(i)+1)=DCTrgb(k1(i)+4,k2(i)+1)-alpha;
elseif diff>0 % B(4,3)小
DCTrgb(k1(i)+3,k2(i)+2)=DCTrgb(k1(i)+3,k2(i)+2)-alpha;
end
end
end
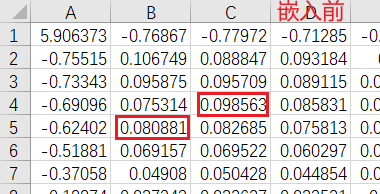
嵌入消息前后DCTrgb矩阵的变化,msg(i,1)==1:
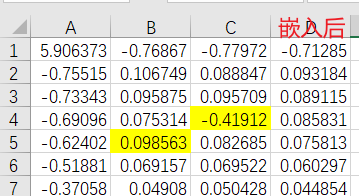
⑤消息写回保存
把嵌入消息的DCTrgb矩阵分块做DCT逆变换,再写回R层,G、B层不变,写回文件,并输出图片查看效果。
% 消息写回保存
DCTrgb_res=DCTrgb;
data_res=blkproc(DCTrgb,[8 8],'P1*x*P2',T',T); % 分块做DCT逆变换
result=data0; % 载体图片double型图像矩阵
result(:,:,1)=data_res; % 更新嵌入信息后的R层
imwrite(result,'DCTres.bmp','bmp');
subplot(2,2,1),imshow(RGB), title('载体图像');
subplot(2,2,2),imshow(data), title('载体图像R层');
subplot(2,2,3),imshow(result), title('嵌入隐藏信息后的图像');
subplot(2,2,4),imshow(data_res), title('嵌入隐藏信息后的图像的R层');

可以看到在嵌入隐藏信息后的图像的R层中有明显的嵌入痕迹,所以在嵌入隐藏信息后的图像中也能隐约看到一些模糊的痕迹。
⑥信息提取
根据之前信息嵌入的过程可以很容易得到信息提取的过程:
- 接收者读取载有秘密信息的图像
- 对图像做DCT变换和分块
- 获得块随机控制的顺序
- 比较$B(u_1,v_1)$和$B(u_2,v_2)$的大小提取秘密信息
- 写回秘密信息
详细代码实现如下,其中对图像做DCT变换和分块和获得块随机控制的顺序与嵌入信息时的步骤相同,只是接收方需要提前从嵌入方获得嵌入信息的大小$count$:
% DCT信息提取
% 从含有隐藏信息的图片中提取秘密信息
clc
clear
secret=imread('DCTres.bmp'); % 装入图像
data0=double(secret)/255; % 将图像矩阵转为double型,因为blkproc的参数要求是double型
data=data0(:,:,1); % 提取r通道中的信息
T=dctmtx(8); % 对图像分块,生成一个8*8 DCT变换矩阵
DCTcheck=blkproc(data,[8 8],'P1*x*P2',T,T'); % 对分块图像做DCT变换,x是每一个分成的8*8大小的块,P1*x*P2相当于像素块的处理函数,p1=T p2=T对,也就是fun=p1*x*p2'=T*x*T'的功能是进行离散余弦变换
% 产生随机的块选择,确定图像块的首地址
[row,col]=size(DCTcheck);
row=floor(row/8); % 分成了8*8的块,共32*32个8*8的块
col=floor(col/8);
a=zeros([row col]); % 32*32的矩阵
key=学号; % 共享密钥
count=96; % 信息的比特数,由藏入方给出
[k1,k2]=randinterval(a,count,key); % 返回随机选择嵌入的行标和列标(对应块)
for i=1:count
k1(1,i)=(k1(1,i)-1)*8+1;
k2(1,i)=(k2(1,i)-1)*8+1;
end
% 准备提取并回写信息
frr=fopen("extract.txt",'w');
for i=1:count
if DCTcheck(k1(i)+4,k2(i)+1) <= DCTcheck(k1(i)+3,k2(i)+2) % B(5,2)<=B(4,3),说明嵌入0
fwrite(frr,0,'ubit1'); % 按位回写
result(i,1)=0;
else % B(5,2)>B(4,3),说明嵌入1
fwrite(frr,1,'ubit1');
result(i,1)=1;
end
end
fclose(frr);
提取秘密信息时就按照消息嵌入时选择的一对系数,比较$B_i(5,2)$和$B_i(4,3)$的大小,如果$B_i(5,2)$大,说明嵌入1;如果$B_i(4,3)$大,说明嵌入0。将提取的信息按位写回extract.txt。
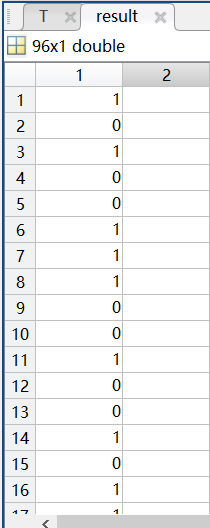
提取结果:

result矩阵中的结果也和msg矩阵中读取的完全相同:
3、分析算法
(这里主要分析自己实现的嵌入“复旦大学”的算法,不分析一种DCT变换数字水印方法.ppt中给出的算法。)
该算法利用DCT变换后系数间的大小关系添加水印信息,实现了水印盲提取,提取水印时不需要原始图像。
并且DCT系数具有特点:
-
直流分量和低频系数值较大,代表了图像的大部分能量,几乎包含了图像信息的90%,对它们做修改会影响图像的视觉效果
-
高频系数值很小,甚至趋向于0,去掉它们基本不引起察觉
接下来基于DCT系数的特点和算法的设计分析算法的不可见性、鲁棒性、容量和安全性。
不可见性
- 算法在选取嵌入位置时,采取在中频部分嵌入水印,中频部分能量适中,能保证较好的不可见性,不像低频系数,由于其所相应的能量过大,秘密消息的不可见性差。
- 算法在选取嵌入位置时特地选择了在JPEG压缩算法中预定义的亮度量化值一样的那些系数的位置。因为量化系数一致,充分表明了位于这两个位置的DCT系数在数量级上是一致的,若产生交换,对图像的破坏较小,保证了不可见性。
- 通过随机间隔法产生随机序列控制信息嵌入位,把秘密信息打散嵌入到图像中,使其不至于在一个局部形成明显的分界线,提升了不可见性
- 根据上述算法,在R通道内嵌入并设置$\alpha=0.5$时,$PSNR=38.6909$,具有不错的不可见性。
鲁棒性
采取在中频部分嵌入水印,中频部分能量适中,不像能量最低的高频部分,容易被篡改,鲁棒性差(比如Jepg有损压缩等操作一般都是针对能量低的高频部分展开的)。
尝试了把生成的DCTres.bmp通过Jepg压缩,仍然能从Jepg文件中提取秘密信息。
容量
将256×256的载体图像分为32×32个8×8的块,图像分块后,可以在每一块中编码一个秘密信息,增加隐藏信息的容量。
安全性
因为选择了随机间隔法,随机序列的种子可以作为密钥,保证了隐藏信息的安全性。
改进措施:
- 可以通过编码,可以压缩秘密信息,减小总体的嵌入量
- 可以对图像进行置乱操作,提升不可见性和鲁棒性
- 提升不可见性:因置乱后的图像是一幅杂乱无章的图像,其无色彩,无纹理,无形状,不易引起载体图像的在色彩、纹理、形状的改变
- 提升鲁棒性:因为攻击者无法轻易地对置乱后的秘密图像进行恢复和统计分析,穷举测试需要巨大计算量。并且可以抵抗攻击者在隐蔽载体上的诸如涂、画、剪切等攻击,因为在提取的时候,需要进行反置乱,攻击者的修改就会分散到画面的各个地方,形成点状的随机噪声,对视觉影响小
- 或许可以将RGB色彩空间转换到$l\alpha\beta$颜色空间再进行DCT变换,因为$l$分量相对于$α$、$β$分量,在影响可视性中的权重最大,同时$lαβ$基本消除颜色空间的强相关性,改变任何分量时无需考虑其他分量的变化。秘密信息可以隐藏在$α$、$β$分量中,提升了不可见性。且对于$l\alpha\beta$颜色空间的分析工具较少,有很好的抗分析性。
4、讨论
因为在上述的算法中,选择了R通道进行嵌入,在信息嵌入时选择了$(5,2)\&(4,3)$这一对系数,并且设置了$\alpha=0.5$,由于好奇如果选择其他做法结果会怎么样,所以下面进行一些控制变量的实验。
①上述算法是在R通道中嵌入信息,尝试在G、B通道中嵌入
data=data0(:,:,1); % 提取R通道做隐藏
data=data0(:,:,2); % 提取G通道做隐藏
data=data0(:,:,3); % 提取B通道做隐藏
经过测试,同样可以正确嵌入和提取秘密信息。
嵌入后结果如图,根据肉眼观察,嵌入B层的不可见性最好,其次是R层,G层的不可见性最差,可以看到明显嵌入的痕迹。

但是三幅图和原图的峰值信噪比相差不大:
| 嵌入R通道 | 嵌入G通道 | 嵌入B通道 | |
|---|---|---|---|
| PSNR | 38.6909 | 38.7265 | 38.6252 |
PSNR的值和人的主观感觉不一致,这是由于PSNR是基于对应像素点间的误差,即基于误差敏感的图像质量评价,并未考虑到人眼的视觉特性(比如人眼对空间频率较低的对比差异敏感度较高,人眼对亮度对比差异的敏感度较色度高,人眼对一个区域的感知结果会受到其周围邻近区域的影响等),所以会出现评价结果与人的主观感觉不一致的情况。
②消息嵌入时,选择$(2,3)\&(4,1)$这一对系数
在消息嵌入部分,代码修改成如下:
% 信息嵌入
temp=0;
alpha=0.5;
for i=1:count
if msg(i,1)==0 % 嵌入0,要求B(2,3)<B(4,1),若不满足则交换位置,因为k1(i)从1开始,所以是+1
if DCTrgb(k1(i)+1,k2(i)+2) > DCTrgb(k1(i)+3,k2(i))
temp=DCTrgb(k1(i)+1,k2(i)+2);
DCTrgb(k1(i)+1,k2(i)+2)=DCTrgb(k1(i)+3,k2(i));
DCTrgb(k1(i)+3,k2(i))=temp;
end
else % 嵌入1,要求B(2,3)>B(4,1),若不满足则交换位置
if DCTrgb(k1(i)+1,k2(i)+2) < DCTrgb(k1(i)+3,k2(i))
temp=DCTrgb(k1(i)+1,k2(i)+2);
DCTrgb(k1(i)+1,k2(i)+2)=DCTrgb(k1(i)+3,k2(i));
DCTrgb(k1(i)+3,k2(i))=temp;
end
end
% 要满足|B(2,3)-B(4,1)|>alpha,如果不满足,把小的系数调整的更小
diff=DCTrgb(k1(i)+1,k2(i)+2)-DCTrgb(k1(i)+3,k2(i));
if diff>=-alpha && diff<=alpha
if diff<0 % B(2,3)小
DCTrgb(k1(i)+1,k2(i)+2)=DCTrgb(k1(i)+1,k2(i)+2)-alpha;
elseif diff>0 % B(4,1)小
DCTrgb(k1(i)+3,k2(i))=DCTrgb(k1(i)+3,k2(i))-alpha;
end
end
end
在消息提取部分,代码修改成如下:
% 准备提取并回写信息
frr=fopen("extract.txt",'w');
for i=1:count
if DCTcheck(k1(i)+1,k2(i)+2) <= DCTcheck(k1(i)+3,k2(i)) % B(2,3)<=B(4,1),说明嵌入0
fwrite(frr,0,'ubit1'); % 按位回写
result(i,1)=0;
else % B(2,3)>B(4,1),说明嵌入1
fwrite(frr,1,'ubit1');
result(i,1)=1;
end
end
嵌入结果如下,肉眼上看两幅图像嵌入结果的不可见性差不多。

峰值信噪比也差不多:
| 选择系数(5,2)&(4,3)嵌入 | 选择系数(2,3)&(4,1) | |
|---|---|---|
| PSNR | 38.6909 | 38.2918 |
因为这两组系数在JPEG压缩算法中预定义的亮度量化值一样,且都是中频系数,所以有良好的不可见性。
如果进行一些离谱选择,比如说把能量最高的直流系数和能量最低的高频系数互换,会产生以下效果,图像很明显地被破坏了。

③$α$的其他取值
| 引入控制量$α$的目的是为了对系数差值进行放大。因为在编码的过程中,无论是$B_i(u_1,v_1)>B_i(u_2,v_2)$,还是$B_i(u_1,v_1)<B_i(u_2,v_2)$,都要使得$ | B_i(u_1,v_1)-B_i(u_2,v_2) | >\alpha$,这样即使在变换过程中系数的值有轻微的改变,也不会影响编码的正确性。 |
设置$α$是有必要的,因为发现消息嵌入后待写回的DCT矩阵DCTrgb_res和消息提取做DCT变换后的DCT矩阵DCTcheck中的数值有些许差别,尤其是第一个8×8块(红框中)中的内容,有一些点甚至发生了$±$0.01的变化:
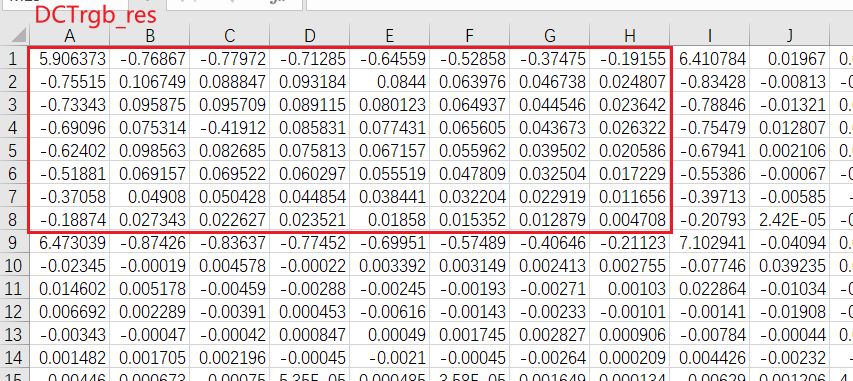
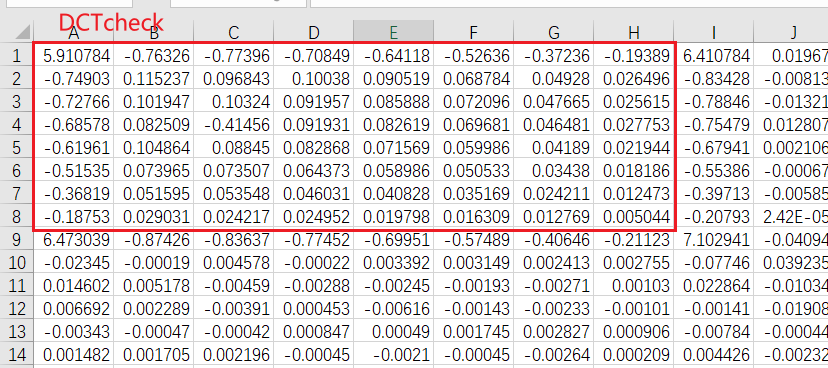
这就意味着设置$α$是必要的,且$α$的值不能设置的太小。
当$\alpha=0$时,即不设置$\alpha$时,可以发现信息提取有误:

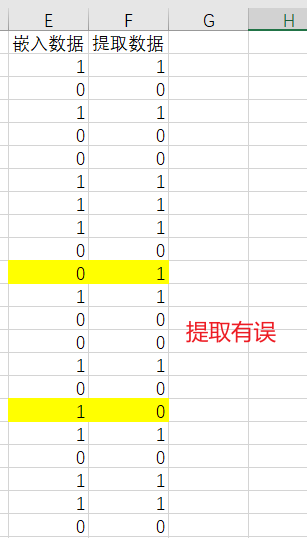
| 并且由于算法设计的是比较$ | B_i(u_1,v_1)-B_i(u_2,v_2) | >\alpha$是否不成立,如果不成立,则将其中小的那个数值$-\alpha$,如果$\alpha$设置过大,则会使得这个调整过于突兀。 |
下图是$\alpha=0.5$时嵌入前后的DCT矩阵对比,可以发现$B(4,3)$的值$-\alpha$后,和周围的点相比还是比较突兀的。
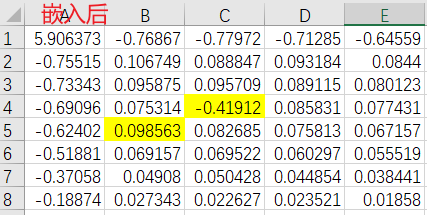
尝试更多$α$的取值,结果如图:
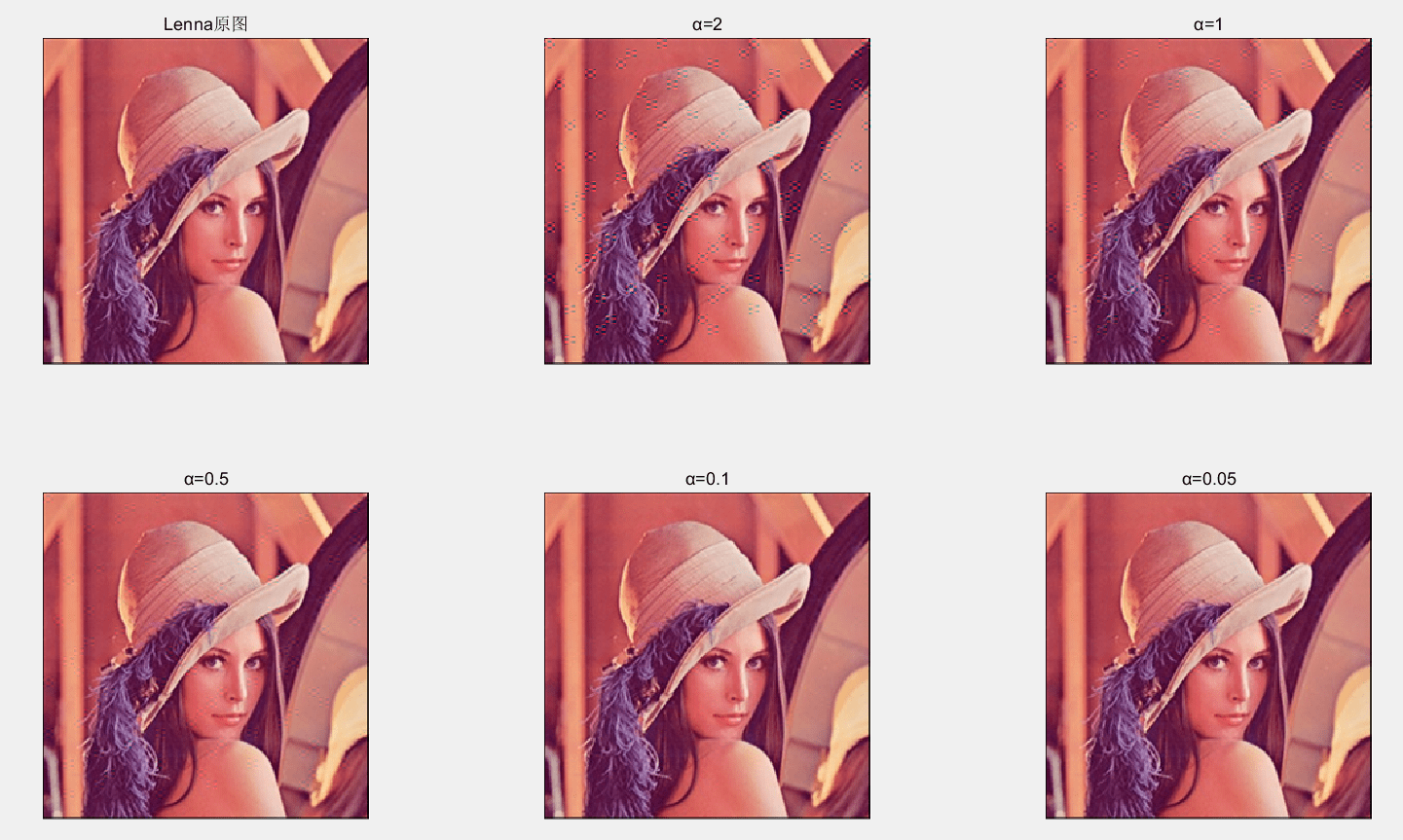
通过肉眼观察可以发现,$α$越小,不可见性越好。当$α=2$时,可以看到明显嵌入痕迹,随着$α$减小,嵌入痕迹逐渐减轻,当$α=0.1$时,肉眼无法区别出和原图的差别。
峰值信噪比同样是随着$α$变小,PSNR变大。
| α=2 | α=1 | α=0.5 | α=0.1 | α=0.05 | |
|---|---|---|---|---|---|
| PSNR | 28.0411 | 33.2333 | 38.6909 | 50.8979 | 53.4083 |
为了均衡鲁棒性和不可见性,算法中还是选择了$α=0.5$。