一、实验要求
设有两幅图像图1 Woman和 图2 Lenna。其中图1是二值图像,作为水印;图2是256灰度图像,作为载体图像。
1、把图1分别隐藏到图2的8个位平面中的一个,并解释结果。
2、如何提高此方法的不可感知性和鲁棒性。
3、提取隐藏的水印。
二、实验过程
(1)隐藏信息
1、通过matlab中的imread函数读取载体图像文件和秘密图像文件(bmp格式)
lenna=imread('Lenna.bmp');
woman=imread('woman.bmp');
2、分别处理秘密图像和载体图像
将载体图像的最低位平面清零,由于第1个位平面由每一个像素最低比特位组成,权重最小,对图片的影响也最小,所以肉眼无法看出前后的变化。
carrier=bitand(lenna,254); % 载体图像和1111,1110进行与运算,置最低1位为0

将秘密图像的最高位平面分离,并移动到最低位平面,方便之后秘密图像的嵌入。由于第8个位平面由每一个像素的最高比特位组成,权重最高,对图片的影响最大,肉眼仍然可以看清其中的主要信息。
highest=bitand(woman,128); % 提取秘密图像最高位
cover=bitshift(highest,-7); % 右移至最低bit位

3、秘密图像和载体图像异或,嵌入秘密信息:
res=bitor(carrier,cover); % 图像隐藏
4、显示并保存处理结果
imwrite(res,'res.bmp','bmp'); % 将图像数据res写入到 "res.bmp" 文件中
subplot(1,3,1),imshow(lenna), title('Lenna原始图像(载体)');
subplot(1,3,2),imshow(woman), title('Woman原始图像(秘密)');
subplot(1,3,3),imshow(res), title('隐藏后的结果');

5、通过类似的做法,可以把秘密图像的最高位平面嵌入到载体图像的不同层,对比效果:
clc % 清理命令行
% hide
lenna=imread('Lenna.bmp');
woman=imread('woman.bmp');
highest=bitand(woman,128); % 提取秘密图像最高位
% 嵌入第1位平面
carrier1=bitand(lenna,254); % 和 1111,1110 进行与运算
cover1=bitshift(highest,-7); % 将秘密图像的最高1bit位右移至最低1bit位
res1=bitor(carrier1,cover1); % 图像隐藏
imwrite(res1,'res1.bmp','bmp'); % 将图像数据res1写入到 "res1.bmp" 文件中
% 嵌入第2位平面
carrier2=bitand(lenna,253); % 和 1111,1101 进行与运算
cover2=bitshift(highest,-6);
res2=bitor(carrier2,cover2);
imwrite(res2,'res2.bmp','bmp');
% 嵌入第3位平面
carrier3=bitand(lenna,251); % 和 1111,1011 进行与运算
cover3=bitshift(highest,-5);
res3=bitor(carrier3,cover3);
imwrite(res3,'res3.bmp','bmp');
% 嵌入第4位平面
carrier4=bitand(lenna,247); % 和 1111,0111 进行与运算
cover4=bitshift(highest,-4);
res4=bitor(carrier4,cover4);
imwrite(res4,'res4.bmp','bmp');
% 嵌入第5位平面
carrier5=bitand(lenna,239); % 和 1110,1111 进行与运算
cover5=bitshift(highest,-3);
res5=bitor(carrier5,cover5);
imwrite(res5,'res5.bmp','bmp');
% 嵌入第6位平面
carrier6=bitand(lenna,223); % 和 1101,1111 进行与运算
cover6=bitshift(highest,-2);
res6=bitor(carrier6,cover6);
imwrite(res6,'res6.bmp','bmp');
% 嵌入第7位平面
carrier7=bitand(lenna,191); % 和 1011,1111 进行与运算
cover7=bitshift(highest,-1);
res7=bitor(carrier7,cover7);
imwrite(res7,'res7.bmp','bmp');
% 嵌入第8位平面
carrier8=bitand(lenna,127); % 和 0111,1111 进行与运算
cover8=bitand(woman,128);
res8=bitor(carrier8,cover8);
imwrite(res8,'res8.bmp','bmp');
subplot(2,4,1),imshow(res1), title('嵌入第1位平面');
subplot(2,4,2),imshow(res2), title('嵌入第2位平面');
subplot(2,4,3),imshow(res3), title('嵌入第3位平面');
subplot(2,4,4),imshow(res4), title('嵌入第4位平面');
subplot(2,4,5),imshow(res5), title('嵌入第5位平面');
subplot(2,4,6),imshow(res6), title('嵌入第6位平面');
subplot(2,4,7),imshow(res7), title('嵌入第7位平面');
subplot(2,4,8),imshow(res8), title('嵌入第8位平面');

可以看到由于第1、2、3位平面的权重较小,对图片的影响较小,当嵌入第1、2、3位平面时,肉眼无法分辨出和原图的差别。从嵌入第4位平面开始,随着像素比特位权重的增加,肉眼可以感觉到图片纹理的变化。当嵌入第6位平面时,可以隐约看到秘密图像的轮廓。嵌入第8位平面时可以明显看到秘密图像,载体图像反而难以辨认出来。
充分说明了8个位平面在图像中所代表的重要程度是不同的。由每一个像素最低比特位组成的第1位平面对于图片的影响最不重要,由最高比特位组成的第8位平面对于图片的影响最重要。
(2)提取隐藏信息
提取过程即隐藏的逆过程。这里以提取隐藏在第1位平面中的信息为例。
由于信息隐藏在第1位平面中,所以先bitand(src1,1)提取最低位的信息,再通过bitshift(secret1,7)左移到高位就可以看到秘密图像。由于秘密图像是二值图像,每个像素只能取0或者255,如果最低位是1,左移到最高位后是128,不是255,可以在左移后的结果上×255,就可以还原秘密图像。(每个像素是8位,最大值是255,这里matlab 128*255不会造成溢出,等于像素的最大取值255)。
% 提取隐藏在第1位平面中的信息
src1=imread('res1.bmp');
secret1=bitand(src1,1); % 提取最低位
secret1=bitshift(secret1,7)*255; % 左移到最高位
subplot(1,1,1),imshow(secret1),title("提取隐藏在第1位平面中的秘密图像")
下面是是否*255的对比,左图没有乘,所以理应是白色的像素目前取值为128,呈现出灰色;右图还原了秘密图像,白色像素均为255。

左图的详细信息,可以看到灰色的点都是128:

右图的详细信息:
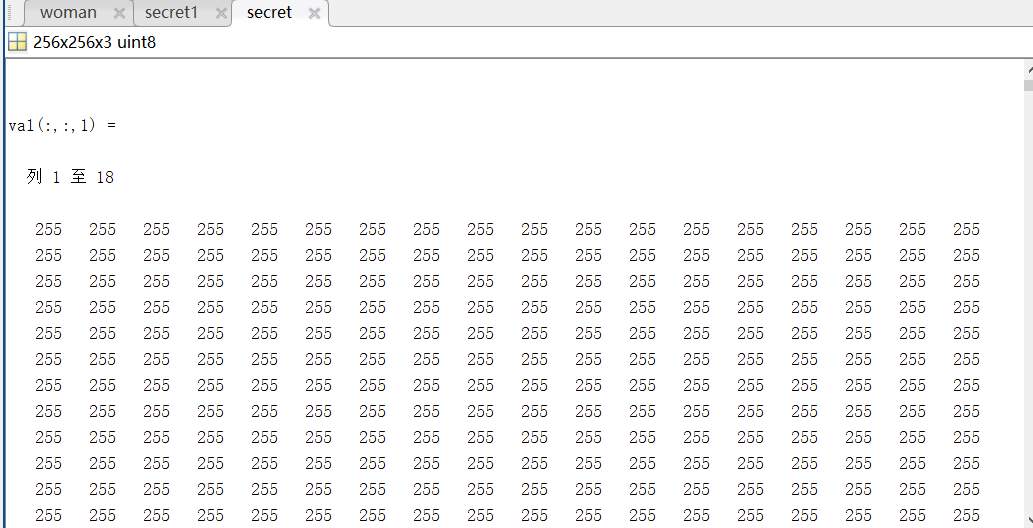
根据上述步骤,类似的可以提取出嵌入在其他层的秘密信息:
clc % 清理命令行
% extract
% 提取隐藏在第1位平面中的信息
src1=imread('res1.bmp');
secret1=bitand(src1,1); % 提取最低位,和 0000,0001 进行与运算
secret1=bitshift(secret1,7)*255; % 左移到最高位
% 提取隐藏在第2位平面中的信息
src2=imread('res2.bmp');
secret2=bitand(src2,2); % 和 0000,0010 进行与运算
secret2=bitshift(secret2,6)*255; % 左移到最高位
% 提取隐藏在第3位平面中的信息
src3=imread('res3.bmp');
secret3=bitand(src3,4); % 和 0000,0100 进行与运算
secret3=bitshift(secret3,5)*255; % 左移到最高位
% 提取隐藏在第4位平面中的信息
src4=imread('res4.bmp');
secret4=bitand(src4,8); % 和 0000,1000 进行与运算
secret4=bitshift(secret4,4)*255; % 左移到最高位
% 提取隐藏在第5位平面中的信息
src5=imread('res5.bmp');
secret5=bitand(src5,16); % 和 0001,0000 进行与运算
secret5=bitshift(secret5,3)*255; % 左移到最高位
% 提取隐藏在第6位平面中的信息
src6=imread('res6.bmp');
secret6=bitand(src6,32); % 和 0010,0000 进行与运算
secret6=bitshift(secret6,2)*255; % 左移到最高位
% 提取隐藏在第7位平面中的信息
src7=imread('res7.bmp');
secret7=bitand(src7,64); % 和 0100,0000 进行与运算
secret7=bitshift(secret7,1)*255; % 左移到最高位
% 提取隐藏在第8位平面中的信息
src8=imread('res8.bmp');
secret8=bitand(src,128)*255; % 提取最高位
subplot(2,4,1),imshow(secret1),title("提取隐藏在第1位平面中的秘密图像")
subplot(2,4,2),imshow(secret2),title("提取隐藏在第2位平面中的秘密图像")
subplot(2,4,3),imshow(secret3),title("提取隐藏在第3位平面中的秘密图像")
subplot(2,4,4),imshow(secret4),title("提取隐藏在第4位平面中的秘密图像")
subplot(2,4,5),imshow(secret5),title("提取隐藏在第5位平面中的秘密图像")
subplot(2,4,6),imshow(secret6),title("提取隐藏在第6位平面中的秘密图像")
subplot(2,4,7),imshow(secret7),title("提取隐藏在第7位平面中的秘密图像")
subplot(2,4,8),imshow(secret8),title("提取隐藏在第8位平面中的秘密图像")
提取结果:

(3)分析算法
LSB方法会把秘密信息嵌入到图片像素的最低位平面,所以不可见性很好。可以计算原始图像和含秘密信息的图像的峰值信噪比衡量图像失真或是噪声水平的客观标准。2个图像之间PSNR值越大,则越相似。普遍基准为30dB,30dB以下的图像劣化较为明显。
lenna=imread('Lenna.bmp');
src1=imread('res1.bmp');
PSNR1=psnr(lenna,src1) % 调用psnr函数计算峰值信噪比
得到的结果如下:
| 嵌入第1位平面 | 嵌入第2位平面 | 嵌入第3位平面 | 嵌入第4位平面 | 嵌入第5位平面 | 嵌入第6位平面 | 嵌入第7位平面 | 嵌入第8位平面 | |
|---|---|---|---|---|---|---|---|---|
| PSNR(dB) | 51.1631 | 45.1296 | 39.1173 | 33.1910 | 27.1078 | 20.9239 | 15.7660 | 8.4908 |
可以看到嵌入最低位平面时,$PSNR>50dB$,不可见行非常好,嵌入第4位平面时PSNR仍然保持在30dB以上,但是嵌入第5位平面之后$PSNR<30dB$,图像劣化明显。随着嵌入位平面的重要性的提升,不可见性逐渐降低。
在鲁棒性上,由于LSB使用了图像不重要的像素位,算法的鲁棒性差,抗干扰性差,水印信息很容易被噪声掩盖,被滤波、图像量化、几何变形等操作破坏。
并且由于嵌入的秘密图片是二值图片,所以只需要嵌入一个位平面,如果嵌入的秘密图片是灰度图像或是彩色图像,上述算法的容量就不太够。
对于提升容量、不可见性和鲁棒性,可以从以下几个角度考虑:
提升容量:
- 通过编码,可以压缩秘密图片,减小总体的嵌入量
- 信息隐藏可以不局限在Bit Plane 0上,将隐藏规则扩展到所有位平面上,实施组合位平面的信息隐藏策略,提升嵌入的信息容量
提升不可见性:
- 对图像进行置乱操作,将秘密图像置乱后嵌入到载体图像,或将载体图像置乱后再嵌入秘密信息,可以增加信息隐藏算法的不可见性,因置乱后的图像是一幅杂乱无章的图像,其无色彩,无纹理,无形状,不易引起载体图像的在色彩、纹理、形状的改变
- 基于$l\alpha\beta$颜色空间设计信息隐藏算法,因为$l$分量相对于$α$、$β$分量,在影响可视性中的权重最大,同时$lαβ$基本消除颜色空间的强相关性,改变任何分量是无需考虑其他分量的变化。秘密信息可以隐藏在$α$、$β$分量中,提升了不可见性。
提升鲁棒性:
- 利用奇偶校验位的方法,用区域LSB的统计特性代替直接替换。嵌入时选择$L(m)$个不重叠区域,计算出每一区域的所有最低比特的奇偶性,并选择一个载体元素的最低比特位存放这个区域的奇偶校验位。因为提取时会计算奇偶校验位和提取的进行比较,起到了验证的作用,提升了鲁棒性。
- 利用Patchwork算法,因为只有水印嵌入者可以对水印进行正确检测,攻击者无法判定图像中是否含有水印。(提升抗分析性)
- 对图像进行置乱操作也可以提升鲁棒性。因为攻击者无法轻易地对置乱后的秘密图像进行恢复和统计分析,穷举测试需要巨大计算量。并且可以抵抗攻击者在隐蔽载体上的诸如涂、画、剪切等攻击,因为在提取的时候,需要进行反置乱,攻击者的修改就会分散到画面的各个地方,形成点状的随机噪声,对视觉影响小。